Thesaurus parvus mathematicus/physicus
7 Basisgrößen
| Größe | Symbol | Einheit | Zeichen |
|---|---|---|---|
| Länge | l | Meter | m |
| Masse | m | Kilogramm | kg |
| Zeit | t | Sekunde | s |
| Stoffmenge | n | Mol | mol |
| Temperatur | T | Kelvin | K |
| elektr. Stromstärke | I | Ampere | A |
| Lichtstärke | Iv | Candela | cd |
Abgeleitete Größen
| Größe | Symbol | Berechnungs- möglichkeit1) |
Einheit | Einheitensymbol SI-Darstellung |
Bemerkung |
|---|---|---|---|---|---|
| Geschwindigkeit | v | l/t | Meter pro Sekunde | m/s | |
| Beschleunigung | a | v/t | Meter pro Sekunde² | m/s² | |
| Impuls | p | m·v | Newton-Sekunde | ||
| Kraft | F | m·a | Newton | ||
| Arbeit | W | F·l | Joule | ||
| elektr. Energie | Eel | Q·U = I·U·t | Joule | 1eV = e·U = 1,602·10-19 C · 1V = 1,602·10-19 C·V = 1,602·10-19 A·s·W/A = 1,602·10-19 A·s·J/(s·A) = 1,602·10-19 J | |
| Fläche | A | l² | Quadratmeter | m² | |
| Volumen | V | l³ | Kubikmeter | m³ | |
| Druck | p | F/A | Pascal | 1 bar = 105 Pa 1 torr ≈ 133,32 Pa = 1,3332 mbar |
|
| Dichte | ρ | m/V | Kilogramm pro Kubikmeter | kg/m³ | 1 g/cm³ = 1000 kg/m³ |
| elektrische Spannung | U | W/Q = R·I | Volt | ||
| elektrischer Widerstand | R | U/I | Ohm | ||
| elektrische Ladung | Q | I·t | Coulomb | C = A·s | |
| elektrische Kapazität | C | Q/U | Farad | 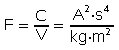 |
|
| elektrische Feldstärke | E | 2) | Volt pro Meter | ||
| magnetische Feldstärke | H | 2) | Ampere pro Meter | A/m | |
| magnetische Flussdichte | B | 2) | Tesla | ||
| Drehmoment | M | F·l | Newtonmeter | ||
| kinetische Energie | Ekin | ½·m·v² | Joule | ||
| potentielle Energie | Epot | m·g·h | Joule | Formel gilt für die pot. Energie einer Masse ggü. einem Bezugspotential (h = Abstand/Höhe, g = Erdbeschleunigung) | |
| Frequenz | f | 1/t | Hertz | Hz = 1/s | |
| Leistung | P | W/t | Watt |
Naturkonstanten
| Größe | Zeichen | Wert | |
|---|---|---|---|
| Atomare Masseneinheit | mu | 1,66053873·1027 kg | |
| Avogadro-Konstante | NA | 6,02214199·1023 mol-1 | |
| Boltzmann-Konstante | kB | 1,3806505·10-23 J/K | |
| Drehimpulsquantum | h/(2π) | 1,054571596·10-34 J·s | |
| Elektrische Elementarladung | e | 1,60217653·10-19 C | |
| Elektrische Feldkonstante | ε0 | 8,854187817·10-12 F/m | |
| Elektronenradius | re | 2,817940285·10-15 m | |
| Faraday-Konstante | F | 9,64853515·104 C/mol | |
| Gaskonstante, molare | R | 8,314472 J/(mol·K) | |
| Gravitationskonstante | G | 6,673·10-11 N·m²/kg² | |
| Kreiskonstante | π | 3,1415926535897932 | |
| Lichtgeschwindigkeit (Vakuum) | c | 2,99792458·108 m/s | |
| Loschmidt-Konstante | NL | 2,6867775·1025 1/m³ | |
| Magnetische Feldkonstante | µ0 | 1,2566370614·10-6 H/m³ | |
| Molares Normvolumen | V | 22,413996·10-3 m³/mol | V = n·R·T/p |
| Normalfallbeschleunigung (Erde) | g | 9,80665 m/s² | |
| Planck-Konstante | h | 6,62606876·1034 J·s | |
| Ruhemasse des Elektrons | me | 9,10938188·10-31 kg | 5,485799110·10-4 u |
| Ruhemasse des Neutrons | mn | 1,67492716·10-27 kg | 1,00866491578 u |
| Ruhemasse des Protons | mp | 1,67262158·10-27 kg | 1,00727646688 u |
| Rydberg-Konstante | R∞ | 1,0973731568549·107 1/m | |
| Stefan-Boltzmann-Konstante | σ | 5,670400·10-8 W/(m²·K4) | |
| Wellenwiderstand (Vakuum) | Γ | 376,7303 Ω | |
| Wien-Konstante | b | 2,897756·10-3 m·K |
Flächen und Volumina
Sofern an den entsprechenden Stellen nicht anders angegeben, gelten in der nachfolgenden Tabelle diese Bezeichnungen:
| Legende | |||
|---|---|---|---|
| r = Radius | h = Höhe | G = Grundfläche | a, b = Katheten |
| geometrische Größe | Formel | Erläuterung |
|---|---|---|
| Dreiecksfläche (allgemein) | ½·hc·c | c = beliebige Seite hc = Höhe (senkrecht auf c) |
| Dreiecksfläche (rechtwinklig) | ½·a·b | |
| Dreiecksfläche (gleichseitig) | ||
| Kreisumfang | 2·π·r | |
| Kreisfläche | π·r² | |
| Ellipsenfläche | π·a·b | a, b = Halbachsen |
| Ellipsenumfang | elliptisches Integral3) | Näherung: 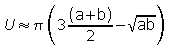 |
| Kugeloberfläche | 4·π·r² | |
| Kugelvolumen | ||
| Ellipsoidenvolumen | a, b, c = Halbachsen | |
| Ellipsoidenoberfläche | elliptisches Integral3) | |
| Pyramidenvolumen | 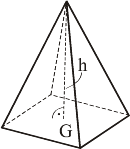 Grundfläche = beliebiges n-Eck |
|
| Kreiskegelvolumen | 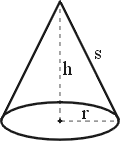 s = Mantellinie s = Mantellinie |
|
| Kreiskegeloberfläche | π·r·(r+s) | |
| Kreiszylindervolumen | π·r²·h | 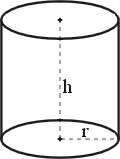 |
| Kreiszylinderoberfläche | 2·π·r·(r+h) | |
| Prismavolumen | G·h | 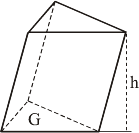 |
| Tetraedervolumen | a = Kantenlänge | |
| Tetraederoberfläche | ||
| Oktaedervolumen | a = Kantenlänge | |
| Oktaederoberfläche | ||
| Dodekaedervolumen | a = Kantenlänge | |
| Dodekaederoberfläche | ||
| Ikosaedervolumen | a = Kantenlänge | |
| Ikosaederoberfläche |
1) Hier sind eine oder mehrere Möglichkeiten zur Berechnung der entsprechenden Größe angegeben. Es ist zu beachten, dass diese u.U. nur für gewisse Sonderfälle bzw. unter vereinfachenden Voraussetzungen gültig sein können, es ist daher immer die Anwendbarkeit zu prüfen und ggf. entsprechende Literatur zu Hilfe zu nehmen.
2) Die Lösungsverfahren der Feldberechnung fußen auf den Maxwellschen Grundgleichungen. Es gibt selbstverständlich zahlreiche Vereinfachungen für spezielle Probleme/Anordnungen, die die Angabe von einfacheren Gleichungen zur Lösung ermöglichen (z.B. ergibt sich das elektrische Feld zwischen zwei parallelen Kondensatorplatten mit Plattenfläche A und Ladung Q unter Vernachlässigung von Randeffekten zu E=Q/εA). Die große Anzahl an möglichen Gleichungen würde allerdings den Rahmen dieser Übersicht sprengen, entsprechende Formelsammlungen sollten hier weiterhelfen. (Für komplexere Probleme exisitieren ausschließlich Näherungen)
3) Die Berechnung führt auf ein elliptisches Integral, welches i.A. nicht elementar lösbar ist, deswegen sei hier auf entsprechende Tafelwerke (wie z.B. Bronstein) verwiesen.