This is about the ciphering of text with the help of matrix products.
It is not really easy but more secure than normal cipher proceedings you can do by hand.
The intrinsically calculating steps you have to do are easy. You can do it in your brain.
For this cipher proceeding you first have to know some general rules.

The product of two matrixes can only be formed if the number of columns of the first matrix is the same as the number of lines of the second matrix.

So the multiplication of these matrixes:

D · C = 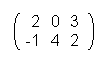· 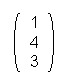is possible with the result ,
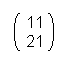but the multiplication of C · D = 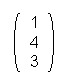· 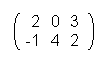is not possible because the number of columns of the first matrix is smaller than the number of lines of the second matrix.

For a matrix A the matrix A^-1 is declared with the property:

A · A^-1 = A^-1 · A = E

By this, E is the neutral element of that multiplication, for example E = 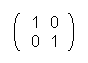is valid for the (2;2) matrixes, a matrix with two columns and two lines.
For the (3;3) matrixes is valid equivalent: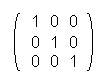

So for (n;n) matrixes is valid:
(n 0 0 0 0 0 ....... 0 n 0 0 0 0 ...... 0 0 n 0 0 0 etc.)

Wanted is the matrix A^-1 for A =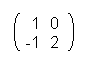

Because of the better legibility you use for matrixes with a small number of elements different letters with only one index.

Here the schema A · A^-1 = A^-1 · A = E is used again. We know E and A so it is reputed to be:

· = <=> = =

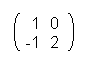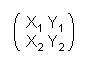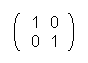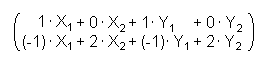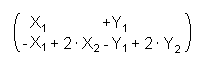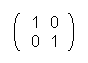
Of the similarity of the matrixes follows:

X₁ = 1       Y₁ = 0
-1 + 2 · X₂ = 0 <=> X₂ = ½        - 0 + 2 · Y₂ = 1 <=> Y₂ = ½

So, valid is:

A^-1 =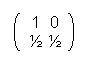


Now we will come to the really interesting part, the ciphering of a sentence.

But first another general information about ciphering.

Cipherings are easy to decipher when the single letters are replaced by another letter. In this case an examination of the frequency of the letters leads fast to the aim. Ciphering with matrixes is hardly to crack. At first every letter of the alphabet gets a number depending on his position in it.

So
A = 1, B = 2...... Z = 26

Now we can choose an optional sentence, for example:

"Big Brother is watching"

Now you have to decide if you want to use a (2;2) matrix or a bigger, more complex one. The more complex the more save the ciphering is.

So, because it is the easiest I choose the (2;2) matrix.

I arrange the sentence to groups of four letters:

BIGB ROTH ERIS WATC HING


Now every letter is assigned to his number and put into a matrix.

So we have:



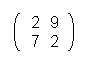
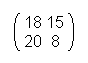
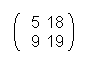
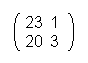
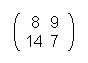
At the end every of that matrixes is multiplied with the ciphering-matrix U.
For example: U = 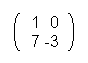. Of course this is exchangeable.

In this example you get:



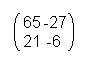
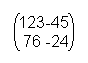
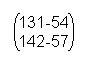
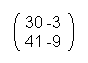
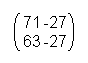
Now you can also see that similar letters aren't assigned to similar numbers. For example the “t”. In one case it has the number 76 and in another the number 41.

To get the original sentence you have to multiply with the matrix U^-1. (So the inverse matrix to U)

The procedure is described above in the text.
So for the Matrix U = 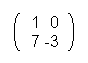you get:

A^-1 = 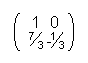= U^-1

By multiplying you get the original matrixes again.

This way of ciphering is very save because everyone who wants to decipher the sentence or text has to know the ciphering matrix. The number of possible matrixes is infinitely. Cause of that it is still hard to decipher with the help of a PC because for every “decipher-matrix” you get a different sentence or text. By reducing the worth of the numbers for the result which cannot be bigger than 26 the number of possibilities is reduced a bit but there are still infinitely possible matrixes.
Of course ciphering of texts with a program like for example PGP is much more easier but ciphering with the just named way you can be done with a pencil and a sheet of paper and is in every case more secure than the most ciphering systems you can do by hand.



Written by [Andi]